Imagining Things
Problem Solving Part 1—Newton's Method and Bisection Method
November 9, 2023 by Klugmeister
29 minute read
This image of "mathematics professor" was created by Klugmeister using artificial intelligence software. The image does not depict a real person. The image was reviewed by Klugmeister before posting on this web page.
I had an epiphany on the topic of "problem solving" when I took courses on "Numerical Analysis" and "Introductory Computer Programming" during college. (Yeah, this post is a bit nerdy but I'll try not to go off the deep end.) I came away from these classes with these conclusions:
- Simpler approaches are preferred over more powerful or more complex approaches in certain situations
- The best approach for solving a problem may be a customized approach that reflects the individual circumstances of the particular problem—if you can identify or potentially anticipate the nature of the problem
- It will help inform your decision-making if you apply a "stress test" to the problem to help identify suitable (or unsuitable) solutions
For background, let's take a look at the methods covered in these classes, and then I promise I'll eventually get back around to the topic of problem-solving. Because this is a rather lengthy post, I'll postpone the discussion of the "Introductory Computer Programming" class to the second installment (Problem Solving Part 2). This first installment only covers the "Numerical Analysis" approaches.
Numerical Analysis—Background
The "Numerical Analysis" class I took in college was a mathematics class focused on using computer approaches to solve math problems numerically. One of our class assignments involved finding all of the zeroes (or "roots") of a complicated function that the professor cooked up. I don't recall the function specifically, but I remember that it was a complex one that included several polynomial terms along with other functions (e.g., ln(x) if I remember right) mixed in as factors. Determining how many zeroes there were was part of the assignment—I want to say the "Frankenstein function" had seven zeroes, but it's hard to be sure since college was sooo 40 years ago. To protect my ego, I won't tell you how many of the seven zeroes I found.
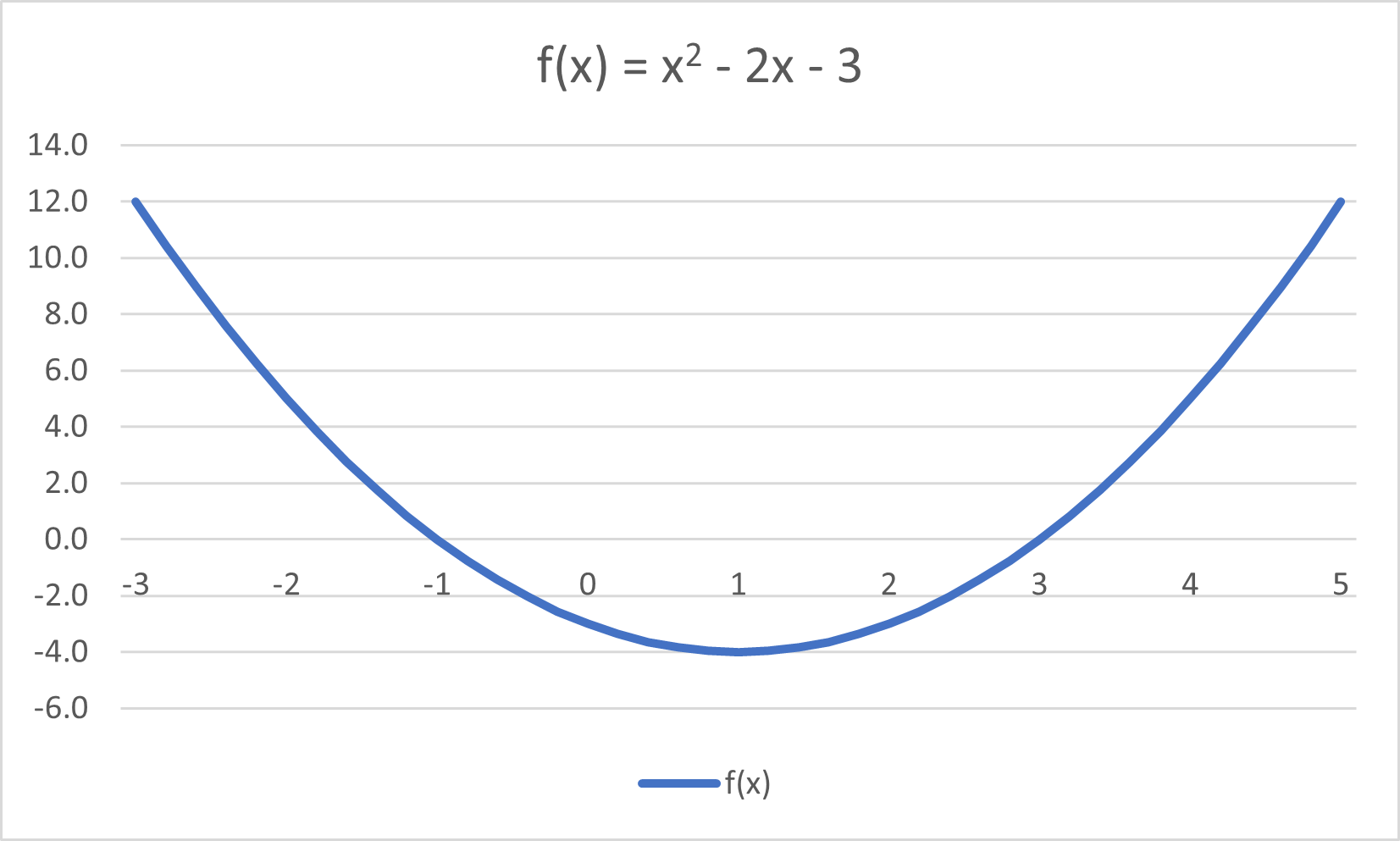
In high school I'd faced similar (but much simpler) algebra problems involving quadratic polynomials that could be solved analytically by factoring. For example, to find the zeroes of f(x) = x2 - 2x - 3 (i.e., to find the values of x for which f(x) = 0), you'd "factor" the equation x2 - 2x - 3 = 0 into two factors, and the zeroes (or "roots") would be the values of x that make one or the other factor equal to zero. (This is based on the concept that if you multiply two numbers and get 0, then it follows that one or the other of the factors must be 0.) The factors are (x - 3)(x + 1) = 0, so the zeroes of the function are x = 3 and x = -1. (The factoring algebra is not shown here. Note you could also use the quadratic equation to get the two zeroes.) Note that this quadratic polynomial was specifically selected so that the zeroes would be integers rather than difficult numbers like 2 1/7 or 3.1415926.
While polynomials of degree 2 (and more generally, with degree of 1 to 4) are solvable analytically, there are no general formulas for solving for the zeroes of polynomials of degree 5 and higher (though some specific ones like x5 - 1 = 0 have easy solutions, i.e. x = 1). Thus, numerical approaches like Newton's method are an important part of one's toolbox for these situations involving higher degree polynomials.
We've included here a graph that illustrates the function curve (a "parabola") which passes through the x axis at x = 3 and x = -1. This graph will help visualize what we're trying to accomplish and will also be helpful once we start illustrating numerical approaches to solving the same problem. (Yes, Scarlet, we're going to solve the problem numerically even though we already know the answers.) It'll take some time, but we'll eventually circle back to our stated topic on problem solving. So buckle up, bub.
Newton's Method—Conceptual Framework
The concept behind Newton's method is to start with an initial approximation x0 of the zero you're seeking. To help prevent unexpected results, it's best to choose an initial estimate that is in the vicinity of the zero you're targeting, using the function's graph as a visual guide. For example, to find the zero of f(x) = x2 - 2x - 3 (the high school function we just introduced) which is at x = 3, you might start at x0 = 4. Next you would imagine a tiny alien on the point (x0, f(x0)) of the function's curve (i.e., (4, 5)) who shoots a ray gun in the direction that the curve is headed in at that point (the red "tangent line" as shown on the accompanying graph). Mark the point where the laser crosses the x axis, and label it x1—it's a new, hopefully closer estimate of the function's zero.
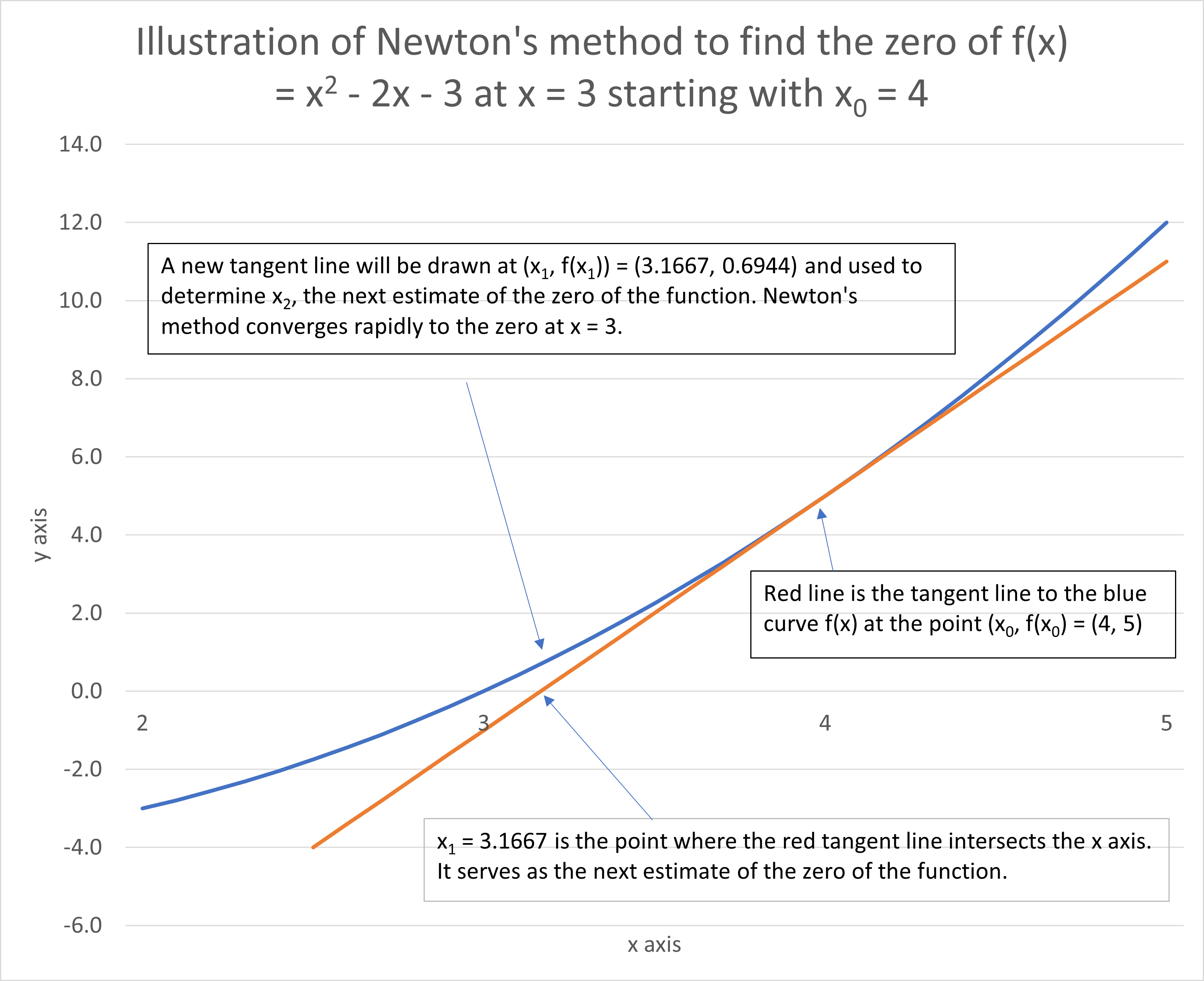
Then you repeat the process by asking the alien to shoot a new tangent line (not shown) from (x1, f(x1)) which crosses the x axis at a new estimate x2 of the function's zero (not shown). If the stars are aligned, the process soon hones in on ("converges" to) the desired zero within a few more iterations. (In fact, as discussed in the next section, x2 is pretty close to 3.)
The process is visually illustrated on the attached graph which shows the function curve, the tangent line at (x0, f(x0)), and x1 and f(x1). Note that the tangent line theoretically only touches the function's graph at a single point (4, 5) but appears to overlap quite a bit because of the thickness of the displayed lines and the wider scale used for the x axis than the y axis. The slope of the tangent line at x0 is f'(x0) which is a calculus concept where the apostrophe indicates the "derivative" of the function.
Newton's Method—Sample Calculations
Now that we've introduced the concept behind Newton's method, we're going to illustrate the method with a few sample calculations. Under Newton's method, you use the recursive formula xn+1 = xn - f(xn) / f'(xn) to generate successive estimates of a zero of the function. (Again, you want to start from an x coordinate that is close to the zero you're seeking.) Thus, starting from an initial guess x0 of one of the function's zeroes, you would subtract from x0: [the value of the function at x0] divided by [the value of the function's derivative at x0]. This yields the next estimate x1, which is then used to find the next estimate x2. This approach is used repeatedly to successively hone in (or "converge") on the zero, or die trying.
We'll illustrate Newton's method with an example based on the now familiar high school function f(x) = x2 - 2x - 3 and its derivative f'(x) = 2x - 2 (the math you'll need to determine the derivative is based on calculus and is not shown here). Let's use x0 = 4 as the initial estimate and see how many iterations it takes to converge on the nearest zero (x = 3). The evaluation of the function and its derivative at x0 = 4 are:
- f(4) = 42 - 2(4) - 3 = 16 - 8 - 3 = 5
- f'(4) = 2(4) - 2 = 8 - 2 = 6
Thus x1 = x0 - f(x0) / f'(x0) = 4 - 5 / 6 = 3.166666 (repeating).
Note we're not at 3 yet, but we're a lot closer! The formula for x2 = x1 - f(x1) / f'(x1) = 3.1666667 - 0.6944444 / 4.3333333, so x2 = 3.0064103. (In only two iterations, we've gotten pretty close to 3.) Proceeding with the next iteration, x3 = 3.0064103 - 0.0256821 / 4.0128205 = 3.0000102. That's the right answer to four decimal places! A very cool thing about Newton's method is that it converges pretty fast! The next iteration (not shown), x4, is correct to at least nine places. Pretty amazing!
As another test of the emergency Newton's method system, we'll separately use x0 = 0 as a starting point and confirm that it converges to the nearby zero x = -1. This time we won't show all the math. If this were a real emergency, the key results would be shown in the table below:
| n | xn | f(xn) | f'(xn) | xn - f(xn) / f'(xn) |
|---|---|---|---|---|
| 0 | 0.0000000 | -3.0000000 | -2.0000000 | -1.5000000 |
| 1 | -1.5000000 | 2.2500000 | -5.0000000 | -1.0500000 |
| 2 | -1.0500000 | 0.2025000 | -4.1000000 | -1.0006098 |
| 3 | -1.0006098 | 0.0024394 | -4.0012195 | -1.0000001 |
| 4 | -1.0000001 | 0.0000004 | -4.0000002 | -1.0000000 |
Note that selecting reasonably good starting estimates is important to the performance of Newton's method, which converged within a few iterations. However, the method may converge even without a favorable initial estimate. For example, a poor selection like x0 = 0.9 would generate an almost horizontal tangent line which would throw x1 all the way out to about -19, and f(x1) all the way up to almost 400! Even so, the method would quickly head back in the direction of x = -1 and would have that zero correct to at least 7 decimal places after eight iterations, as shown in the following table.
| n | xn | f(xn) | f'(xn) | xn - f(xn) / f'(xn) |
|---|---|---|---|---|
| 0 | -0.9000000 | -3.9900000 | -0.2000000 | -19.0500000 |
| 1 | -19.0500000 | 398.0025000 | -40.1000000 | -9.1247506 |
| 2 | -9.1247506 | 98.5105752 | -20.2495012 | -4.2599110 |
| 3 | -4.2599110 | 23.6666642 | -10.5198221 | -2.0101901 |
| 4 | -2.0101901 | 5.0612444 | -6.0203802 | -1.1695049 |
| 5 | -1.1695049 | 0.7067516 | -4.3390098 | -1.0066218 |
| 6 | -1.0066218 | 0.0265309 | -4.0132435 | -1.0000109 |
| 7 | -1.0000109 | 0.0000437 | -4.0000219 | -1.0000000 |
It's interesting that Newton's Method can make a stop in Minneapolis during a trip from Georgia to California and still get there reasonably fast!
Newton's Method—Discussion and Convergence
Newton's method is a powerful approach which converges rapidly, but it is not without challenges. Below are several characteristics of Newton's method:
- The method assumes that the function f(x) has a continuous derivative
- The iterative Newton's method formula xn shown above assumes that you can calculate the formula for the derivative of the function f'(x) directly (which was the case with the sample high school function we used for illustration purposes, but is not always the case)
- As noted previously, Newton's method may not converge if the initial estimate is too far away from a root. As a result, it may be prudent to stop running the iteration algorithm (regardless of outcome) after about 10 iterations to avoid an infinite computer loop
- Newton's method won't converge if it reaches an iteration where f'(xn) = 0. This is because a horizontal tangent line will not intersect the x axis.
- The further bad news is significant: Newton's method may not converge at all, and it's hard to tell beforehand when this might happen. As Homer Simpson would say, "Doh!"
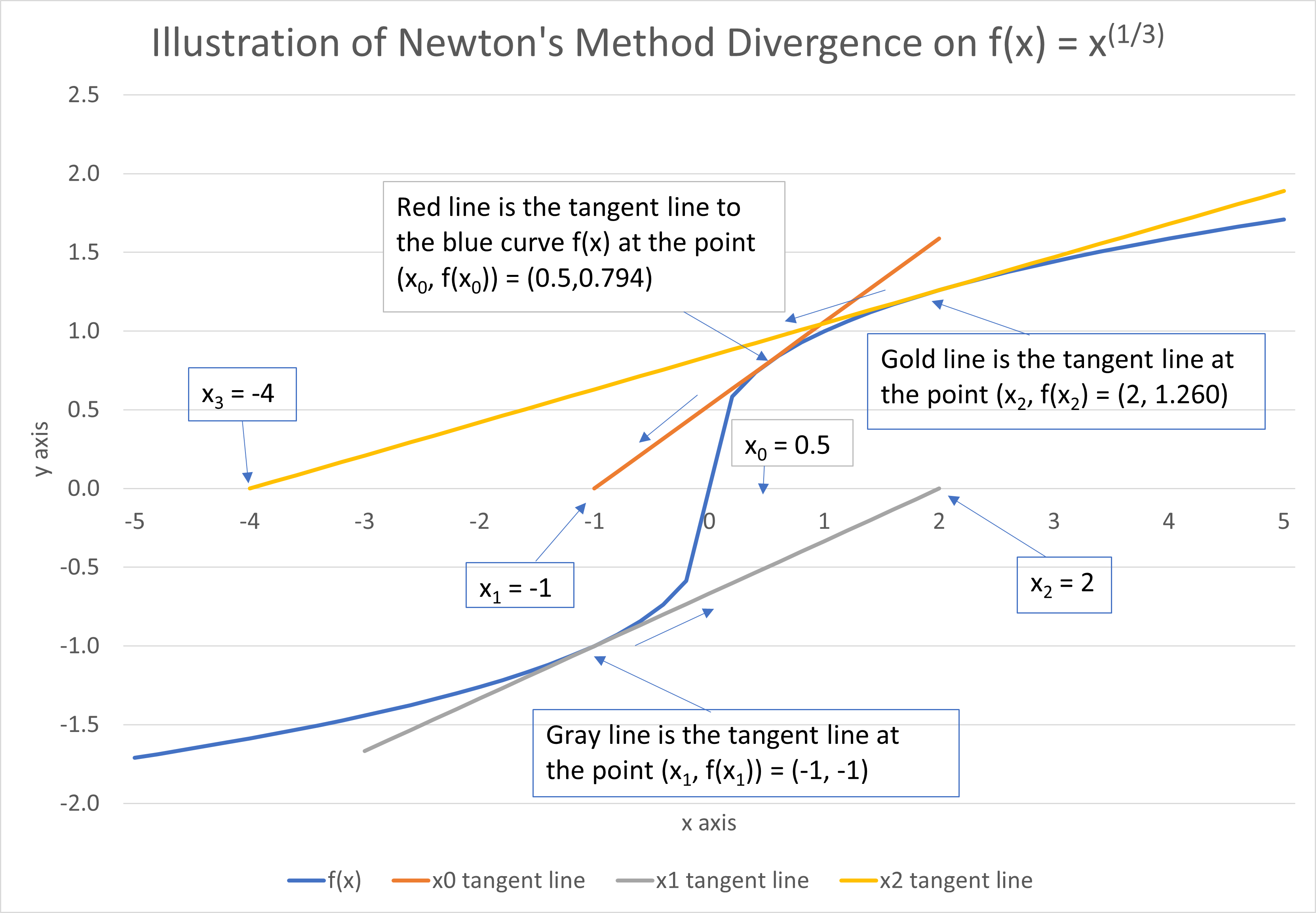
An example of a function that does not converge at all is f(x) = x1/3, also known as the cube root of x. Instead of getting closer to the function's zero (which is at x = 0), the iterations grow increasingly further away! In other words, the method doesn't converge—it diverges! Even starting at an initial estimate that is already close to 0 (say, x0 = 0.5), the estimates are increasingly further away from the zero.
The attached graph illustrates the divergence. Starting with x0 = 0.5, suppose a tiny alien posts himself at the point on the blue curve f(x) = x1/3 with x = 0.5 (i.e. on (0.5, 0.794)). He then shoots his ray gun toward the x axis along the red tangent line at that point. The tangent line intersects the x axis at x = -1 —this is x1, the next estimate. The tiny alien reposts himself on the blue curve at (x1, f(x1)) = (-1, -1), then shoots the ray gun along the gray tangent line at that point, landing at x2 = 2. The process continues, with each estimate getting twice as far away from the desired zero at x = 0. As it turns out, Newton's method does not converge to x = 0 for any starting point x0 (unless you start with the answer, i.e. x0 = 0)! Given the first bullet point listed above, this is perhaps not surprising—because the derivative of f(x) is undefined at x = 0 (the tangent line is a vertical line with infinite slope), the function fails the requirement that it have a continuous derivative.
Bisection Method—Conceptual Framework
This blog post is getting long in the tooth, so I'm going to go into less detail with the bisection method for finding zeroes of functions than for Newton's method.
The concept behind the bisection method is to divide an interval that is known to contain a zero of the function in half, and then to determine which half the zero is in (which I'll explain in a moment). You then repeat the process starting with the new interval (which is now half the width of the original interval). You can stop the process when the interval is small enough to show the zero to the number of decimal places you desire.
The bisection method is rather like a tortoise in that it is slow to converge.
Bisection Method—Sample Calculations
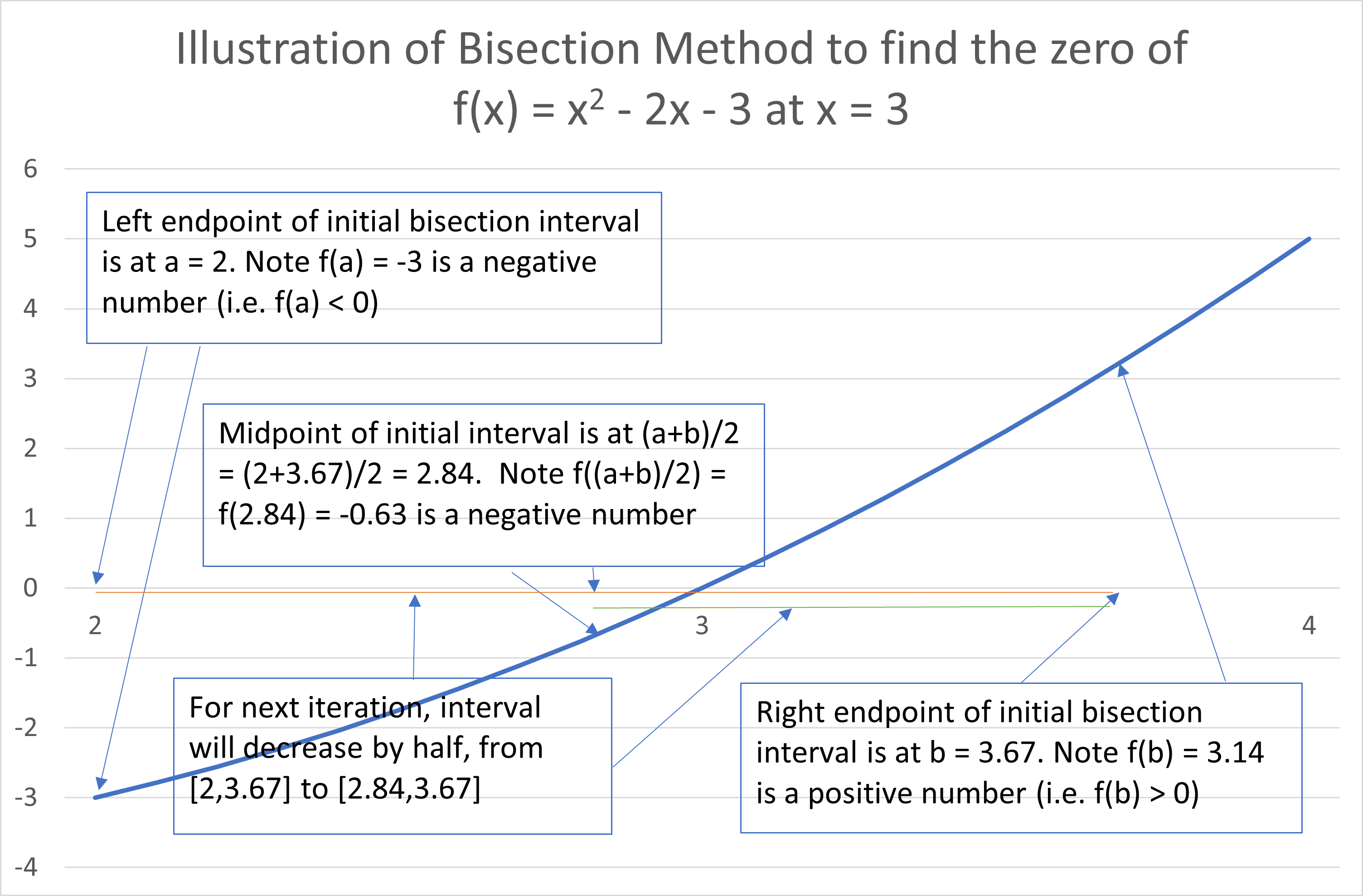
Attached is an example illustrating an iteration of the bisection method on our now familiar high school function f(x) = x2 - 2x - 3, focused on the zero at x = 3. To start, we select an interval that is known to contain a zero of the function. You can do this by eyeballing the graph of the function (the blue curve on the attached graph) and noting the general vicinity where the function's curve crosses the x axis. Let's go with a left endpoint of a = 2 and a right endpoint of b = 3.672518 (note I picked a weird number so the calcs aren't too easy)— note this interval clearly contains the zero that we're pretending we don't already know is at x = 3. As a check, note that f(a) and f(b) have opposite signs—this is what we want, because if one point is negative and the other is positive, the curve must cross the x axis somewhere in between. f(a) = f(2) = -3, and f(b) = f(3.672518) = 3.142353, so we can check the box for "f(a) and f(b) have opposite signs." The initial interval from 2 to 3.672518 is shown on the graph by the red line segment.
We now find the midpoint of the interval: (a+b)/2 = (2 + 3.672518) / 2 = 2.836259. We then evaluate the function at that point to determine whether f((a+b)/2) is negative or positive. f(2.836259) = -0.628153 is negative. We then establish (a+b)/2 as an endpoint of a new interval that is half the width of the original interval. But which half of the original interval do we keep, and which do we discard? In other words, should (a+b)/2 be the new left endpoint or the new right endpoint?
We discard whichever endpoint has the same sign as f((a+b)/2) since we want the function's values at the new endpoints to have opposite signs in order to ensure there's a zero in between. In our case, f((a+b)/2) has the same sign as f(a) (i.e., they're both negative), so we discard a and replace it with (a+b)/2 as the new left endpoint. So our new interval is a = 2.836259 to b = 3.672518 (shown as the green line segment on the graph). Note f(a) = -0.628153 and f(b) = 3.142353 have opposite signs, so that is confirmation that we chose the correct half of the interval. Note also that the width of the new interval 0.836259 ( = 3.672518 - 2.836259) is half the width of the initial interval 1.672518 ( = 3.672518 - 2.000000). The interval is still so wide as to not be useful for identifying the zero at x = 3, but note that the width of the interval will be cut in half with each successive iteration of the bisection method.
Recognizing that the explanation in the previous paragraph seems a bit thick, I can summarize the selection of the new interval using the following logic:
- Calculate f((a+b)/2)
- If f((a+b)/2) has the same sign as f(a), discard a as the left endpoint and make (a+b)/2 the left endpoint of the new interval (the "new" a)—note this is the logic that applied for this iteration
- If f((a+b)/2) has the same sign as f(b), discard b as the right endpoint and make (a+b)/2 the right endpoint of the new interval (the "new" b)
We keep repeating the process until the interval is sufficiently small to determine the zero to the desired number of decimal places. We essentially "sandwich" the answer inside increasingly small intervals until they're so small that we know the answer to the desired level of precision. We also stop iterating if the bisection approach lands on the zero exactly (i.e. if f((a+b)/2) = 0).
Below is a table of values reflecting several iterations of the bisection method.
| n | a | b | (a+b)/2 | f(a) | f(b) | f((a+b)/2) |
|---|---|---|---|---|---|---|
| 0 | 2.000000 | 3.672518 | 2.836259 | -3.000000 | 3.142353 | -0.628153 |
| 1 | 2.836259 | 3.672518 | 3.254389 | -0.628153 | 3.142353 | 1.082268 |
| 2 | 2.836259 | 3.254389 | 3.045324 | -0.628153 | 1.082268 | 0.183349 |
| 3 | 2.836259 | 3.045324 | 2.940791 | -0.628153 | 0.183349 | -0.233329 |
| 4 | 2.940791 | 3.045324 | 2.993058 | -0.233329 | 0.183349 | -0.027721 |
| 5 | 2.993058 | 3.045324 | 3.019191 | -0.027721 | 0.183349 | 0.077131 |
| 6 | 2.993058 | 3.019191 | 3.006124 | -0.027721 | 0.077131 | 0.024534 |
| 7 | 2.993058 | 3.006124 | 2.999591 | -0.027721 | 0.024534 | -0.001636 |
| 8 | 2.999591 | 3.006124 | 3.002858 | -0.001636 | 0.024534 | 0.011438 |
| 9 | 2.999591 | 3.002858 |
Note that the zero at x = 3 has been calculated to within two decimal places after eight iterations. (Observe that when we round a and b to two decimal places, we get 3.00 in each case.) In contrast, Newton's method had the answer to four decimal places after only three iterations—i.e., it took fewer iterations to get the answer to more decimal places. The bisection method is much slower to converge than Newton's method.
Selecting a Method: Newton's Method vs. Bisection Method
If you were given the assignment to find the several zeroes of the Frankenstein function, which approach(es) would you choose?

This image of "photograph of an alien shooting a ray gun, wide shot" was created by Klugmeister using artificial intelligence software. The image was reviewed by Klugmeister before posting on this web page.
If you're like twentyish me, you would choose the very powerful and quickly converging method named after Sir Isaac Newton! Admittedly, the method as described in class didn't include a tiny alien shooting a ray gun that hones in on the answer so fast it'll make your head spin, but can't you picture it? And who would choose the clearly subpar bisection method that sounds like a strange new birthing method and converges so slowly that it's like watching grass grow? It's like picking whether you want Patrick Mahomes or Mr. Tudball as your quarterback, is it not?
After taking the class, however, I began to question the strategy of always using the most powerful (or flamboyant) approach without giving it a moment's thought. Sure, some of the zeroes of the Frankenstein function could be found easily using Newton's method, but my numerical analysis professor pointed out that Newton's method doesn't always converge, while the bisection method always finds the zero in the initial interval if the function is continuous (which isn't too much to ask) and f(a) and f(b) are of opposite signs. Being twentysomething and naive, I found that the professor's warning that Newton's method sometimes doesn't converge went in one of my ears and out the other.
And who'da thought the professor would "sandbag" the project with some zeroes that couldn't be found using Newton's method? Uh, duh—I should've seen that coming instead of whining about it as if he'd pulled a fast one on the class! What professor doesn't test you on an important topic? Frankly, it was my mistake in judgment to mentally pigeonhole the bisection method as a feeble approach and an unimportant topic. Looking back, it seems like twentyish me was tragically like Homer Simpson when he said "I never dreamt when I gave them my credit card number that they'd charge me."
Sure, it's easy to get mesmerized by the tiny alien shooting the ray gun, but what if the tiny alien occasionally shoots blanks or misses the target completely? That really limits the usefulness of Newton's method. Would you rely on a cooking approach if, say, 90% of the time the food is delicious, but 10% of the time the food doesn't get cooked at all? In fact, it's so easy to get caught up in the seemingly fabulous Newton's method, that when it doesn't work you may sit around like a lost puppy wondering what to do, when you should be reaching into your toolkit and pulling out the unflashy but reliable bisection method!
And yeah—the bisection method converges slowly—big deal! Let's not forget that a computer is doing the heavy lifting, so even if it takes four times as long to converge, that may only translate to enough extra time for you to take another sip of coffee (with milk—no sugar). Puh-lease—it's not like Newton's method works in a millisecond while the bisection method takes several hours. In fact, one of the most impressive characteristics of the bisection method is that, while the zero can run from the bisection method, it can't hide!! With each successive iteration, the bisection method eliminates half of the remaining real estate while the increasingly nervous cockroach expresses astonishment that this allegedly subpar method is eventually going to find its exact location and hit it with Raid. The reliability of the bisection method for finding the zero ought to count for something, but oftentimes we scratch our heads and leave Mr. Reliable in the toolbox. Then again, I scratch my head over many things, including why Ben Affleck always seems to be able to find good-looking women who want to marry him.
Problem Solving Implications
Inspired by my nerdy college math class on numerical analysis from 40 years ago, I've found the following three problem-solving strategies to be helpful in real life:
- Don't count out simple approaches
- Customize the approach
- Apply a stress test
Let's tackle these problem-solving strategies one at the time.
1. Don't Count Out Simple Approaches
A simple approach may be the best solution to the problem at hand, depending on the circumstances. If instead you always use a more complicated approach, you may be wasting time and resources and not getting a better outcome. This is especially true if the simple approach is very reliable while the complex approach is not.

This image of "American football player group tackle" (our effort to depict "three yards and a cloud of dust") was created by Klugmeister using artificial intelligence software. The image was reviewed by Klugmeister before posting on this web page.
An example of a simple approach is paying off credit card debt using a "three yards and a cloud of dust" approach. It's not exciting, but to pay off your credit card debt you may just need to buckle down and make those payments month after month while not incurring any more charges. It's awfully boring, and yes—it would be so great if you could just snap your fingers and make the credit card balances disappear quicker, but some problems take time to be solved, and in these cases simply grinding ahead is a pretty effective strategy. Other fancy approaches—e.g., moving balances all over place—may make you feel like you're accomplishing something (because you're engaging in lots of activity), especially if you're a Type A person, but may just be obscuring the fact that you're not making progress.
In fact, the Type A person may pursue a strategy of making aggressive payments toward the credit card while still continuing to use it, but this can be a recipe for disaster if you're not very disciplined. Wouldn't it be better to just pay $200 toward your credit cards (and not charge anything new) than to pay $1,200 and charge up a new $1,000? Sure, the net impact is the same ($1,200 minus $1,000 = $200), but the bigger risk here is that you could optimistically believe you can pay $1,200 and that makes you feel like you're making progress, all while you actually charged $2,000 and dug yourself a bigger hole. (For the non-mathematically inclined who didn't catch the point, $1,200 minus $2,000 is -$800, so you added $800 to your balance rather than paying it down.) And if you're not a bean-counter by nature, you may not even realize where the line of scrimmage is, and that you're losing yardage rather than gaining it! Like the imaginary alien shooting the ray gun in Newton's method, you may be getting farther away from the target instead of closer.
The bottom line is that fancy or flamboyant approaches may have a reliability problem when used by people who aren't disciplined. Sure, it feels awfully impressive to Type A people to score 7 touchdowns in a game, but if you take defense lightly and the other team scores 9 touchdowns, you don't win—you lose!
2. Customize the Approach
To the extent you can identify or potentially anticipate the nature of the problem, it can help you craft an appropriate solution. Football coaches do this all the time, by anticipating the type of play the other coach will run, and designing a strategy to counteract it. You don't have to know what the other coach is going to do—it may pay off if you even make your best guess. Don't discount the importance of being thoughtful. In fact, it's helpful to anticipate what plays the specific team (and coaches) you're facing may call rather than general situations (e.g., x% of all teams blitz on third down, so a screen pass might work effectively).
The idea of tailoring the solution to the problem is an important one in other areas, such as providing financial or investment advice. For example, it's expected that a financial advisor will meet with his or her new client to gather information about the client's goals and risk tolerance prior to making any investment recommendations. In fact, to recommend an investment without first gathering this type of information is a risky move that could potentially expose the financial advisor to litigation, especially if the investment doesn't work out as expected. Sure, an investment advisor may be convinced that he or she is recommending a plain vanilla investment that could be suitable for most anyone, but doing so before gathering the client information is a nutty thing to do, and everyone knows it.
And yet, I find that many people don't embrace the importance of gathering information about the individual when they are giving other types of advice, such as relationship advice. People will often dish out shrink-wrapped relationship advice that's meant to work for most of the people most of the time, rather than tailoring it to the specific person they're giving the advice to. These same people that would cry foul if someone gave them investment advice without individualizing it, and would sue the wannabe investment advisor from here to kingdom come, may nevertheless have no qualms about handing out shrink-wrapped relationship advice like it was candy. I daresay relationship advice that would be suitable if you were married to Denzel Washington may very well be unsuitable if you're married to Ike Turner, and vice versa. Frankly I believe it's a mistake to provide advice that ought to work for most of the people most of the time (i.e., the same advice you'd give anyone else), rather than tailoring it to the specific person you're giving the advice to.
3. Apply a Stress Test
It is good practice to "kick the tires" on the proposed solutions to problems. Are there situations that the proposed solution would address particularly well or not so well? We saw this with Newton's Method vs. the bisection method, where one of the desirable traits of the bisection method (i.e., its dependability) helped fill the void in exactly the type of situations where Newton's method fails (i.e., sometimes it doesn't converge to the desired zero at all).
Let's take the example of a homeowner who's considering whether to open a home equity line of credit (HELOC). Since HELOCs are a type of revolving loan that is secured by the home, they typically feature a favorable interest rate—much lower than the rate on an unsecured personal loan. Being secured by a valuable asset, HELOCs are relatively low risk for the lender. These credit lines offer a convenient way for homeowners with significant equity in their homes to tap that equity for cash. In fact, the lender may allow the homeowner to access the credit line via convenience checks, which are almost as easy as going to the ATM. Of course, amounts drawn against the credit line and not subsequently paid off reduce the proceeds the homeowner will receive from the house upon the eventual sale.
So, what's not to like? Well, the feature that makes the loan relatively safe for the lender (i.e., it's secured by your house) makes it risky for you. If for any reason you are unable to pay the loan back, the lender can foreclose on your house; so, by taking out a HELOC, you are basically putting your home at risk if there are any hiccups on paying it back. In addition, if you're undisciplined in how you use the HELOC, it can be easy to max out your credit line, which can make it difficult to sell your house if the market value isn't enough to cover your mortgage and your HELOC.
So...what could happen to prevent you from paying the loan back? For example, an unexpected job loss could remove your source of funds for paying off the loan. This would perhaps be manageable if the period of job loss is short, but a short period of joblessness can't be guaranteed, and a lengthy job loss is problematic unless you have an adequate emergency fund. Naturally, during a period of job loss, you'd want to prioritize payments toward your mortgage and HELOC over other types of payments (e.g., credit cards, unsecured loans) in order to avoid losing your house, but it can be challenging to sustain these payments for an extended period. While HELOCs may work out just fine for most of the people most of the time, you should kick the tires on what could go wrong and consider whether it's worth the risk. Your house is a valuable asset, so it's important not to treat it like it's a wadded up sheet of paper, a turd, or some other worthless item.
Full disclosure: In the past I've had a HELOC, but I'm not crazy about HELOCs as a borrowing strategy. Of course, it might make sense for a person with lots of home equity and a need for cash to use this strategy, but it feels like it shouldn't be the "go to" strategy for most people.
Previous All Blog Entries Next